数据结构作业五 Compression
图片有损压缩大作业
问题分析 & 解决方案
本次编程任务给出了一个纯英文的PDF文件,较为详细地介绍了图像有损压缩算法的实现方式,通过二叉树的树剪枝达到保留图片细节的目的。任务要求达到的效果如下图所示,可以看出较为复杂的图腾部分得到了很好的保留,而树叶和远处的背景则被明显地压缩成了像素区块。

和编程任务一同给出的源码包中已经实现了绝大部分代码,我们需要按照给出的方法对缺失的代码进行补充,从这方面来讲,整个编程任务相当于一个稍微复杂的程序填空题。另外不得不提的一点是,所给的源码格式较为规范,仔细研究代码的整体框架对日后的编程也有一定的好处,也正因其规范性,代码整体阅读难度较低。
总体来看,整个工程由五个部分组成,其从属关系为:PNG类包含RGBAPixel类,并且通过loadpng中的函数对图片进行最底层的读写。twoDtree通过一个PNG类进行构建,stats在构建的过程中起到辅助作用,加快整个构建过程。程序的宏观框架大致如此,stats中的所有函数都要我们对其进行具体实现,twoDtree中的大部分关键代码都要我们对其进行补充,而其余的三个文件在了解了类的定义方式及大致的成员函数的用法之后便可不必深究。
不难看出,任务只要求对twoDtree和stats两个部分进行补充,刚好将整个任务分为两个部分,由于twoDtree对stats有一定依赖性,首先处理stats的部分。
算法设计
此前已经叙述清楚,任务可以被分为两个部分,接下来对两个部分算法的设计进行说明。
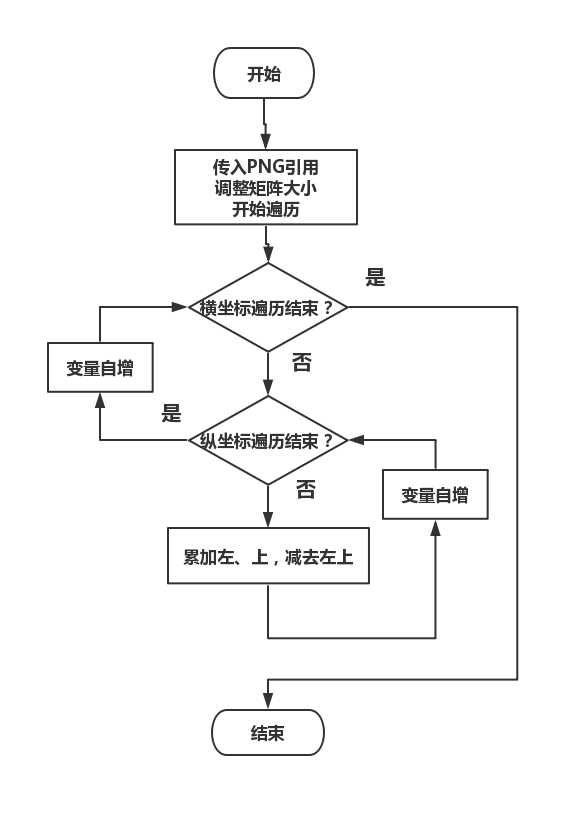
stats类函数的实现
从任务说明中可以了解到,stats类是通过对图片各个通道的像素值进行预计算,使生成二叉树时每种分割情况下计算variability measurement 的复杂度降到常数时间,并能够返回指定小矩阵的多种信息。其中最大的难点便是如何进行预计算使下面的公式降低到常数时间。这里,为了计算方便我们使用等式右边的公式。
$$\sum(x-\bar x)^{2}=\sum x^{2}-\frac{(\sum x)^{2}}{\left| R \right|}$$
结合stats中已经定义的六个二维矩阵不难想到对整个图片各个通道的颜色值及其平方进行累加,如果我们采用当前点的值等于位于该点上方和左侧的两个值及自身三个值累加的方式对整个图片进行递推计算的话,算到最终结果之后会发现很难对这个生成的二维向量进行高效的利用,因为多次累了重复值,起初不明显,等到面积增大之后就会变成很难处理的问题。
稍加思考(hhh,花了将近一个小时)之后我们得到了另外的一种方法,既然我们之前的问题是每计算一个点的值都会导致之前的值被重复计算,为了解决它,我们在计算的时候直接减去会被重复计算的点,这样,最终生成的二维向量中的每个值都等于以原点和当前点确定的矩形中的所有点的累加。
具体实现为:在计算一个点的值的时候,除了加上其上方和左侧的两个点,还要减去左上方的点,按照这个规则进行递推计算,最终的结果就是我们想要的情况。
对于生成矩阵的利用我们用图形进行解释:如图所示,我们已经得到了我们所需的累加和矩阵,矩阵中的每个点的值都等于该点与原点确定的矩形中所有点的累加和。现在我们想要计算出图中绿色矩形所对应的累加和。
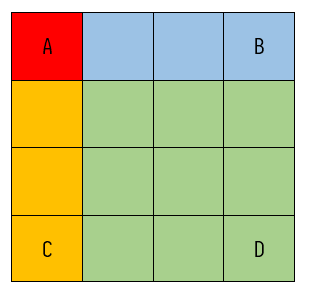
直观来看,sum = 整体 - 蓝色 - 橙色 - 红色
已知: 整体 = D, 蓝色 = B - A,橙色 = C - A,红色 = A
则不难推出,sum = D - B - C + A
按照上述公式我们便可以在常数时间内计算出任何子矩阵对应的累加和。为了方便后续的计算,我在处理矩阵的时候多开辟了额外的空间并存上零,简化了代码。
twoDtree的探索
twoDtree中主要让我们实现的功能有两个,建树和剪枝,至于从树还原到图片和树的基础操作函数是相对基本的内容,通过课上的学习以及对程序框架的理解应该可以很轻松地写出来,在这里不浪费笔墨一个个进行阐述。
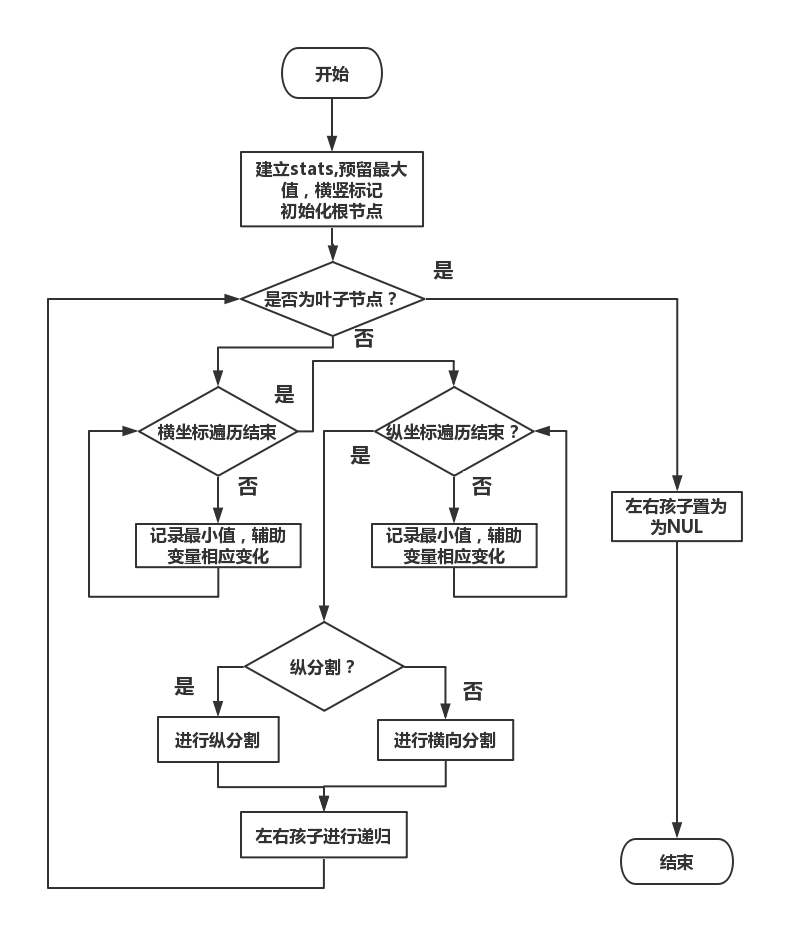
建树函数buildTree
通过对程序的阅读我们可以了解到,二叉树是从图片构建来的,而buildTree便是构造树的关键函数,我们可以把树的一般初始化先在构造函数内写出来,提前准备好该函数需要的参数,之后在构造函数中对其进行调用,生成整个树的框架。
首先审视一下作业PDF中对树的构造方法的解释,我理解的方法是:父节点对应于一个大矩形,如果这个大矩形内有大于两个的像素值,我们就要对它进行分割,划为两个矩形,使两个子矩阵的色彩多样性(我反正这么叫)之和达到最小,这两个矩形就分别对应于左右孩子,这里需要注意左右孩子的顺序。这个过程需要一直执行下去,直到图片中的每个像素都对应于树的叶子节点。需要注意,由于我们不是对称切分,所以最终生成的树并不会是理想结构,我们只能保证的一点是,这个树是一个真二叉树。
这样我们要做的事情就很清楚了,无非就是从根节点开始这个过程,每到一个节点都假设一条虚拟的线,对这个矩形进行切割,分别计算两个矩形的色彩多样性之和,考虑完所有的横纵情况后选择最好的那种。按着这条线切割后继续进行这个过程,直到分为单个像素点。关于如何在常数时间内计算出一个矩形的色彩多样性,我们在stats相关内容中已经进行了说明。
剪枝函数prune
在我看来,这个函数是整个问题最难的点,因为我想不到一个高效的算法只遍历一遍叶子节点。
如何剪枝?一个子树的根节点像素值便是这个子树对应矩形所有像素值的平均,我们要做的事情是计算出这个矩形中和各通道色值与平均值差的平方的和小于等于tolerance的个数,然后计算这一部分像素占像素总个数的比例,如果大于给定值,就代表这个矩形中像素之间的差异不大,我们就可以将这个子树的枝叶剪掉,只留下根节点。反映到图形上来,就是将这个矩形的颜色涂成了平均值。
最终的实现方法很简单,先进行层序遍历,对遍历到的每个节点再进行一次遍历,统计满足条件叶子的个数,最后计算比例,判断是否需要删除。但是这个程序中有这么一句话,让我以为有超级简单的算法可以实现这个过程。但是很不幸,最终还是没有找到。
Pruning criteria should be evaluated on the original tree, not on a pruned subtree. (we only expect that trees would be pruned once.)
流程图
编程实现
stats.cpp
#include <iostream>
#include "stats.h"
using namespace std;
using namespace cs221util;
stats::stats(PNG &im){
//resize
unsigned width = im.width();
unsigned height = im.height();
sumRed.resize(width+1, vector<long>(height+1, 0));
sumGreen.resize(width+1, vector<long>(height+1, 0));
sumBlue.resize(width+1, vector<long>(height+1, 0));
sumsqRed.resize(width+1, vector<long>(height+1, 0));
sumsqGreen.resize(width+1, vector<long>(height+1, 0));
sumsqBlue.resize(width+1, vector<long>(height+1, 0));
RGBAPixel *tmp ;
// sumRed[0][0] = int(tmp->r);
// sumGreen[0][0] = int(tmp->g);
// sumBlue[0][0] = int(tmp->b);
// sumsqRed[0][0] = int(tmp->r)*int(tmp->r);
// sumsqBlue[0][0] = int(tmp->b)*int(tmp->b);
// sumsqGreen[0][0] = int(tmp->g)*int(tmp->g);
// for(int i = 1; i < im.width; i++){
// tmp = im.getPixel(i,0);
// sumRed[i][0] = int(tmp->r);
// sumGreen[i][0] = int(tmp->g);
// sumBlue[i][0] = int(tmp->b);
// sumsqRed[i][0] = int(tmp->r)*int(tmp->r);
// sumsqBlue[i][0] = int(tmp->b)*int(tmp->b);
// sumsqGreen[i][0] = int(tmp->g)*int(tmp->g);
// }
// for(int i = 1; i < im.height; i++){
// tmp = im.getPixel(0, i);
// sumRed[0][i] = int(tmp->r);
// sumGreen[0][i] = int(tmp->g);
// sumBlue[0][i] = int(tmp->b);
// sumsqRed[0][i] = int(tmp->r)*int(tmp->r);
// sumsqBlue[0][i] = int(tmp->b)*int(tmp->b);
// sumsqGreen[0][i] = int(tmp->g)*int(tmp->g);
// }
for(unsigned int i = 1; i <= width; i++)
for(unsigned int j = 1; j <= height; j++){
tmp = im.getPixel(i-1, j-1);
sumRed[i][j] = (int)(tmp->r) + sumRed[i-1][j] + sumRed[i][j-1] - sumRed[i-1][j-1];
sumGreen[i][j] = (int)(tmp->g) + sumGreen[i-1][j] + sumGreen[i][j-1] - sumGreen[i-1][j-1];
sumBlue[i][j] = (int)(tmp->b) + sumBlue[i-1][j] + sumBlue[i][j-1] - sumBlue[i-1][j-1];
sumsqRed[i][j] = (int)(tmp->r)*(int)(tmp->r) + sumsqRed[i-1][j] + sumsqRed[i][j-1] - sumsqRed[i-1][j-1];
sumsqBlue[i][j] = (int)(tmp->b)*(int)(tmp->b) + sumsqBlue[i-1][j] + sumsqBlue[i][j-1] - sumsqBlue[i-1][j-1];
sumsqGreen[i][j] = (int)(tmp->g)*(int)(tmp->g) + sumsqGreen[i-1][j] + sumsqGreen[i][j-1] - sumsqGreen[i-1][j-1];
}
//没有必要强转为int...
}
long stats::getSum(char channel, pair<int, int> ul, pair<int, int> lr){
long ans = 0;
switch (channel)
{
case 'r':
/* code */
ans = sumRed[lr.first+1][lr.second+1];
ans -= sumRed[ul.first][lr.second+1];
ans -= sumRed[lr.first+1][ul.second];
ans += sumRed[ul.first][ul.second];
break;
case 'g':
ans = sumGreen[lr.first+1][lr.second+1];
ans -= sumGreen[ul.first][lr.second+1];
ans -= sumGreen[lr.first+1][ul.second];
ans += sumGreen[ul.first][ul.second];
break;
case 'b':
ans = sumBlue[lr.first+1][lr.second+1];
ans -= sumBlue[ul.first][lr.second+1];
ans -= sumBlue[lr.first+1][ul.second];
ans += sumBlue[ul.first][ul.second];
break;
default:
break;
}
return ans;
}
long stats::getSumSq(char channel, pair<int,int> ul, pair<int,int> lr){
long ans = 0;
switch (channel)
{
case 'r':
/* code */
ans = sumsqRed[lr.first+1][lr.second+1];
ans -= sumsqRed[ul.first][lr.second+1];
ans -= sumsqRed[lr.first+1][ul.second];
ans += sumsqRed[ul.first][ul.second];
break;
case 'g':
ans = sumsqGreen[lr.first+1][lr.second+1];
ans -= sumsqGreen[ul.first][lr.second+1];
ans -= sumsqGreen[lr.first+1][ul.second];
ans += sumsqGreen[ul.first][ul.second];
break;
case 'b':
ans = sumsqBlue[lr.first+1][lr.second+1];
ans -= sumsqBlue[ul.first][lr.second+1];
ans -= sumsqBlue[lr.first+1][ul.second];
ans += sumsqBlue[ul.first][ul.second];
break;
default:
break;
}
return ans;
}
long stats::rectArea(pair<int,int> ul, pair<int,int> lr){
return (lr.first-ul.first+1)*(lr.second-ul.second+1);
}
RGBAPixel stats::getAvg(pair<int,int> ul, pair<int,int> lr){
long sum = rectArea(ul, lr);
long sum_r, sum_g, sum_b;
sum_r = getSum('r', ul, lr) / sum;
sum_g = getSum('g', ul, lr) / sum;
sum_b = getSum('b', ul, lr) / sum;
return RGBAPixel(sum_r, sum_g, sum_b);
}
long stats::getScore(pair<int,int> ul, pair<int,int> lr){
long sum = rectArea(ul, lr);
long sum_r, sum_g, sum_b;
long sumsq_r, sumsq_g, sumsq_b;
sum_r = getSum('r', ul, lr);
sum_g = getSum('g', ul, lr);
sum_b = getSum('b', ul, lr);
sumsq_r = getSumSq('r', ul, lr);
sumsq_g = getSumSq('g', ul, lr);
sumsq_b = getSumSq('b', ul, lr);
//alpha置一?
//是否考虑溢出?
sum_r = sum_r * sum_r / sum;
sum_g = sum_g * sum_g / sum;
sum_b = sum_b * sum_b / sum;
sumsq_r -= sum_r;
sumsq_g -= sum_g;
sumsq_b -= sum_b;
return sumsq_r + sumsq_g + sumsq_b;
}
twoDtree.cpp
/**
*
* twoDtree (pa3)
* slight modification of a Kd tree of dimension 2.
* twoDtree.cpp
* This file will be used for grading.
*
*/
#include "twoDtree.h"
#include <stack>
#include <queue>
/* given */
twoDtree::Node::Node(pair<int,int> ul, pair<int,int> lr, RGBAPixel a)
:upLeft(ul),lowRight(lr),avg(a),left(NULL),right(NULL)
{}
/* given */
twoDtree::~twoDtree(){
clear();
}
/* given */
twoDtree::twoDtree(const twoDtree & other) {
copy(other);
}
/* given */
twoDtree & twoDtree::operator=(const twoDtree & rhs){
if (this != &rhs) {
clear();
copy(rhs);
}
return *this;
}
twoDtree::twoDtree(PNG & imIn){
/* your code here */
height = imIn.height();
width = imIn.width();
stats my_stat(imIn);
pair<int, int> cur_ul, cur_lr;
cur_ul = make_pair(0,0);
cur_lr = make_pair(width-1, height-1);
//注意坐标从零开始
root = buildTree(my_stat, cur_ul, cur_lr);
}
twoDtree::Node * twoDtree::buildTree(stats & s, pair<int,int> ul, pair<int,int> lr) {
/* your code here */
Node *cur = new Node(ul, lr, s.getAvg(ul, lr));
//遍历所有情况
//if(s.rectArea(ul,lr) > 1){ 条件导致死循环
if(ul != lr){
bool flag = 1; //1 means horizontal 0 means vertical
int line = 0;
long tmp;
long Min = 9999999999;
for(int i = ul.second; i < lr.second; i++){
tmp = s.getScore(ul, pair<int,int> (lr.first, i)) + s.getScore(pair<int,int> (ul.first, i+1),lr);
if(tmp < Min){
Min = tmp;
line = i;
}
}
for(int i = ul.first; i < lr.first; i++){
tmp = s.getScore(ul, pair<int,int> (i,lr.second)) + s.getScore(pair<int,int>(i+1, ul.second), lr);
if((i == ul.first && ul.second == ul.first) || tmp < Min){
flag = 0;
Min = tmp;
line = i;
}
}
if(flag){
cur->left = buildTree(s, ul, pair<int,int>(lr.first, line));
cur->right = buildTree(s, pair<int,int>(ul.first, line+1), lr);
}
else{
cur->left = buildTree(s, ul, pair<int,int>(line, lr.second));
cur->right = buildTree(s, pair<int,int>(line+1,ul.second), lr);
}
}
else{
cur->left = NULL;
cur->right = NULL;
}
return cur;
}
PNG twoDtree::render(){
/* your code here */
PNG res(width, height);
renderHelper(res, root);
return res;
}
void twoDtree::renderHelper(PNG& res, Node* cur_node){
if(!cur_node) return; //稍微多余
if(cur_node->left == cur_node->right){
//只有两个都是空也就是叶子节点才会进行操作
for(int i = cur_node->upLeft.first; i <= cur_node->lowRight.first; i++)
for(int j = cur_node->upLeft.second; j <= cur_node->lowRight.second; j++){
*res.getPixel(i, j) = cur_node->avg;
}
return ;
}
else{
renderHelper(res, cur_node->left);
renderHelper(res, cur_node->right);
}
}
void twoDtree::prune(double pct, int tol){
/* your code here */
//先逐层遍历,对每个节点判断是否需要剪枝
queue<Node*> traverse_save;
Node* cur;
int sum, total; //小于tol个数,矩形像素数
double rate;
traverse_save.push(root);
while(!traverse_save.empty()){
cur = traverse_save.front();
traverse_save.pop();
if(cur == NULL)
continue;
sum = pruneHelper(cur, tol, cur->avg);
total = (cur->lowRight.first-cur->upLeft.first+1)*(cur->lowRight.second-cur->upLeft.second+1);
rate = sum / total;
if(rate >= pct){
removeNode(cur->left);
cur->left = NULL;
removeNode(cur->right);
cur->right = NULL;
}
else{
traverse_save.push(cur->left);
traverse_save.push(cur->right);
}
}
}
int twoDtree::pruneHelper(Node* cur, int tol, RGBAPixel avg){
if(!cur)
return 0;
//只计算叶子
if(cur->left == NULL && cur->right == NULL){
long diff = (avg.r - cur->avg.r)*(avg.r - cur->avg.r) + (avg.g - cur->avg.g)*(avg.g - cur->avg.g) + (avg.b - cur->avg.b);
if(diff <= tol)
return 1;
else return 0;
}
return pruneHelper(cur->left, tol, avg) + pruneHelper(cur->right, tol, avg);
}
void twoDtree::clear() {
/* your code here */
removeNode(root);
root = NULL;
}
void twoDtree::removeNode(Node * x){
if(!x) return ;
removeNode(x->left);
removeNode(x->right);
delete x;
return ;
}
void twoDtree::copy(const twoDtree & orig){
/* your code here */
//已经对copy进行了说明,不需要进行空间释放
//本程序中仅有两次调用,调用之前都保证空间已经被初始化
height = orig.height;
width = orig.width;
root = copyNode(orig.root);
}
twoDtree::Node* twoDtree::copyNode(const Node* x){
if(!x) return NULL;
Node *tmp = new Node(x->upLeft, x->lowRight, x->avg);
tmp->left = copyNode(x->left);
tmp->right = copyNode(x->right);
return tmp;
}
结果分析
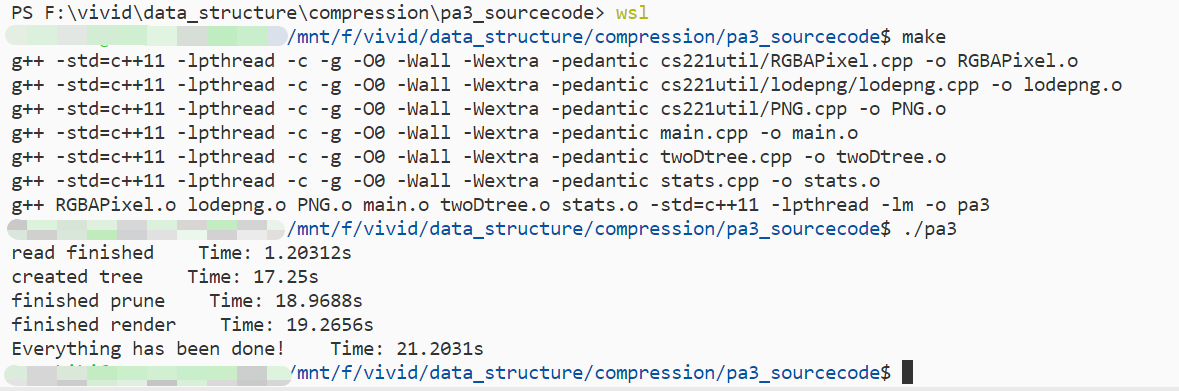
程序在wsl下编译完成,在main函数中添加了显示时间的部分代码,从编译到程序结束的整个过程如下图,对wsl用户名进行了一下处理,不过不影响观察。
下面简单说一下图片的生成情况,自己程序生成的图片和示例图片取得了大体一致的效果,但在细节保留方面以及图片美观程度上稍逊一筹。两个人像画都能做到近乎一致的保留,但稍加观察便可发现细节保留上的差距,下图右侧嘴唇部分处理远不如左侧(效果示例)。

两组图腾的图片,细节较多的图片效果直在几处微小处出现了不同,因为大多数像素都被保留不具备较大的对比价值,在这里不进行详细对比。而另一张则表现出了极大的差别。很容易看出,树丛的细节在我的程序中删除的程度较重,误差最大的一部分甚至直接出现了较大的单色矩形块。

简单分析
我个人认为我的代码实现没有太大的问题,都满足了题目的要求。所给代码中给定的pct和tol值可能适合于跑出示例图片的代码,对我的代码达到不了较好的保存程度。这点是可以理解的。
不同人有不同的实现方式,不同的实现会带来不同的效果,横切还是竖切的选择,数据的计算表达式的书写方式等因素都会带来影响,涉及到浮点数,计算机内部采用的是近似计算,起初微小的误差经历后续计算之后可能会放大很多倍。所以效果有偏差是情理之中的事情。
对于最后图腾图片的较大色块问题,假如参数真的一致,那就应该是我的算法有一些漏洞,细节处理时有一定的问题。
总结体会
我用了一周的时间去想高效的剪枝遍历解决方式,失败之后采用我起初认为最笨最麻烦的方式实现了剪枝函数,最终的运行时间另我很意外,我感觉我一直都在低估自己电脑的运算能力,大多数情况都只停留于感觉,没有进行较为科学的判断和推理,今后应该加强自己这方面的估算能力。另外如果可以的话,我想知道有没有更高效的算法,因为四张图片17秒的速度还是很慢。😕
另外在帮别人调试代码的时候发现了win和linux下long型所占内存的不同,这导致两种环境下long型对应的最大值也不同,在win下编译出来的程序在计算过程中会直接越界,需要换用long long 类型。这次编程因为之前没有用vscode建过工程所以使用wsl进行的编译。程序中有部分代码直接在win下编译也会有一点点小问题,这难道也是linux的优势🐎?